2022/03/19 做题记录

CF617E

发现 $[l,r]$ 中是否有字区间异或和为 k 等价与前缀和 $[l-1,r]$ 中是否有两个位置不同的数异或为 k 直接莫队即可。

code: /code/2022.3.18/CF617E.cpp

Lyndon 分解

$s$ 是 Lyndon Word 表示 $s$ 是其所有后缀中的最小者。

这等价它是自己的最小表示法，因为所有后缀大于它，那么这些后缀加上一个循环后的前缀也一定大于它。

如果 $a,b$ 均为 Lyndon Word 且$a<b$,那么 $a+b$ 也为 Lyndon Word

包含 $a$ 中的字符的 $a+b$ 的后缀一定包含一段 $a$ 的后缀，而这一段后缀一定严格大于 $a$。

而不包含 $a$ 中的字符的后缀一定是 $b$ 或者 $b$ 的后缀，而 b 的后缀一定大于 b，所以我们只需要证明 $a+b<b$。

若 $|a| > |b|$ 或$|a| \le |b|$ 且 $a$ 不是 $b$ 的前缀，那么 $a,b$ 一定在前 $|b|$/$|a|$ 位有不同，得证。

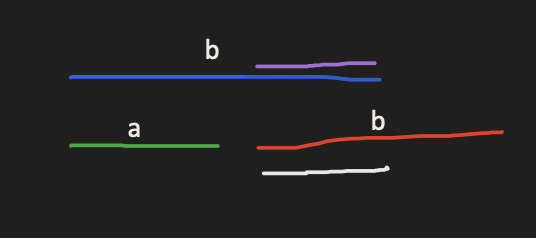
否则若 $a+b \ge b$，

一定存在 $b$ 被涂成白色的前缀大于 $b$ 被涂成紫色的长度相等的后缀，与 $b$ 是自己的最小表示法矛盾，原命题得证。

一个串的 Lyndon 分解一定存在

起初将每一个字符分为一段（一个字符一定为 Lyndon Word），若存在 $s_i,s_{i+1}$ 是的 $s_i < s_{i+1}$，则将其合并。

一个串的 Lyndon 分解唯一

若一个串存在两个不同的 Lyndon 分解，则找到第一个两边分法不相同的段。

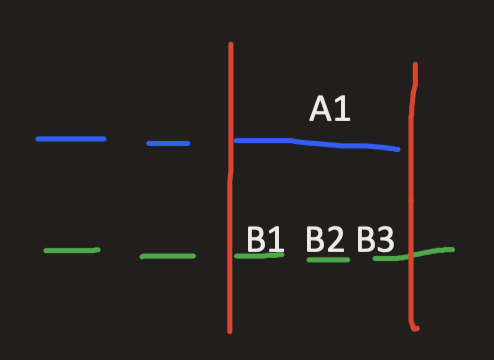
存在：

• B3>A1 (Lyndon 串性质)
• B1>B2>B3 (Lyndon 分解性质)
• A1>B1 (前缀)

推出 A1>A1 , 矛盾。

一个 Lyndon 串的真前缀加上一个比原串中下一个字符大的字符仍是 Lyndon 串

对于一个 Lyndon 串 $s$ 的每一个前缀 $p+d=s$ ，$p$ 的每一个后缀$x$都可以通过加上 $d$来得到原串的一个后缀，因为有 $p+d < x+d$，所以 $p<x$，所以 $p$ 也为 Lyndon 串，而提高最后一个字符的字典序只会提高每一个后缀的字典序列，原串在比较中不会用到这一位(因为后缀的长度不够)。

算法

我们发现如果存在两个相邻的 Lyndon 串 $a,b$ 使得 $a>b$，那么一定不会再发生跨越这两个串的合并，如果我们是顺序合并的，也就代表 $a$ 及之前的分解已经被确定。

那么我们可以假设我们只有一个 Lyndon 串，正在尝试向后合并

如果加入一个字符后这个 Lyndon 串外的字符不再是这个 Lyndon 串的前缀，

(1) 如果新加入的字符小于 Lyndon 串对应位置的字符，那么这段目前还不完整的字符在最终合并后也一定小于这个 Lyndon 串，那么我们就可以把前面的 Lyndon 串添加到已确定的分解中。

(2) 如果新加入的字符大于 Lyndon 串对应位置的字符，通过前面说的，我们可以知道 Lyndon 串外的字符也是一个 Lyndon 串且大于前面的 Lyndon 串，将这两个合并即可。

而剩余的情况就是加入的字符正好和原 Lyndon 串对应相等，这样我们无法确定后面是否有字符能使得 (1) 或 (2) 发生，所以我们就继续循环，而这样我们维护的就是一个 Lyndon 串的循环和后面的一些字符，这样也不会破坏 (1) 和 (2) 的性质（只是合并一个变成了合并所有），如果所有字符都加入完了，就当成 （1）即可。

实现上来说，就是维护 $i$ 表示第一个 Lyndon 串第一个字符的位置，$k$ 表示当前加入的字符，$j$ 表示当前字符在上一个 Lyndon 串中对应的字符，这样我们用 $k-j$ 就可以得到一个 Lyndon 串的长度。

$j$ 的维护也只需要在 (2) 发生，循环改变时重置到 $i$ 即可。

code: /code/2022.3.18/P6114.cpp

CF494B

KMP 算出所有出现的位置后直接树状数组（好像也可以前缀和）优化 dp

$dp_i$ 表示最后一个区间右端点小于等于 i 的方案数

这题怎么这么没意思 /yun

code: /code/2022.3.18/CF494B.cpp