2022/04/21 做题记录

【集训队作业2018】小Z的礼物

Min-Max 容斥后可以得到答案：

$$\sum_{\emptyset \neq S \subset T } (-1)^{|S|}\frac{n*m*2-n-m}{F(S)}$$

其中 T 是所有喜欢的格子，F(S) 是覆盖了任何一个 S 中的格子的相邻格子的对数，而分子就是所有相邻格子的对数。

考虑轮廓线 dp。

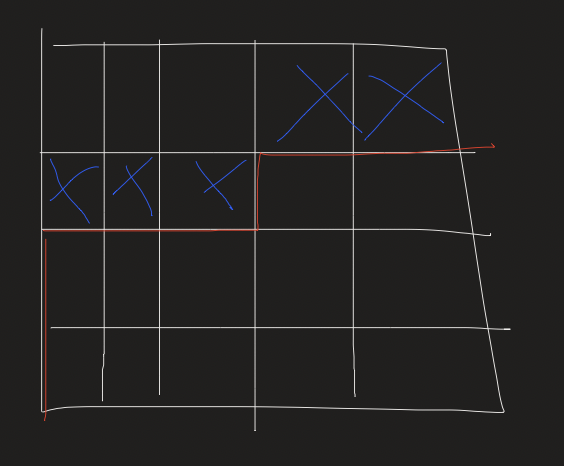
我们一个一个格子的转移，假设我们已经转移完了上面的 8 个格子，那么现在的 dp[s][i] 就是表示那 5 个被打叉的格子选的状态是 s ，已经确定 i 对格子会覆盖我们钦定的格子的时候带容斥系数的方案数，转移就是选不选这个格子，如果选的话我们可以通过轮廓线上的状态确定会新增几对格子。

之后枚举 F(S) 统计即可。

code: /code/2022.4.21/422.cpp

CF914G

可以飞别算出 $s_a | s_b = i$ 且 $s_a \& s_b=0$ 的方案数,$s_c = i$ 的方案数，$s_d\ \text{xor}\ s_e=i$ 的方案数，给它们分别乘个 $fib_i$ 然后或卷积卷起来就行。

code: /code/2022.4.21/CF914G.cpp

地震后的幻想乡

我们可以枚举边的相对大小关系，然后从小到大加入，那么加入到第 i 条边时图第一次联通答案就是 $\frac{i}{m+1}$，于是我们可以计算加入 i 条边图还没联通的方案数 F(x)，而这 i 条边是前 i 小的边的概率是 $\frac{1}{m \choose i}$，于是答案就是 $\frac{1}{m+1} \sum_{i=0}^{m} \frac{F(i)}{m \choose i}$,设 $G(i) = {m \choose i}-F(i)$ 为加入 i 条边图联通的方案数。

可以考虑状压 dp 设 f[S][i] 为 S 这个点集再加入 i 条两端都在 S 内的边不联通的方案数，g[S][i] 同理,num[S] 为两端都在 S 内的边的数量，之后 dp 求 f 的时候枚举任何一个节点所在的联通块就行，g 可以直接用总数减。

code: /code/2022.4.21/P3343.cpp

IIIDX

依赖关系可以建出一颗树，我们把难度从小到大排序，然后从小到大遍历每一个点 x ，那么一个难度可以放在这个点的条件就是大于等于它的数至少有 siz[x] 个，我们可以用线段树维护大于每个数的个数，对于小于等于 x 的就是一个区间减，而对于大于等于 x 的不好处理，因为它们可能不连续，我们设这个线段树维护的每个数为 $a_i$,显然 $a_i$ 连续，那么实际上我们就要删除 $a_j \in (a_i-siz,a_i )$ ，其中 $a_i$ 是我们放到当前节点的数，于是我们可以给 $a_i$ 取一个前缀 min，那么取被删除的就一定不如取权值真的为 $a_i - siz$ 的数了（因为它的难度更大），而对于相等的数我们每次取最左边的可以保证我们维护的权值不出错，前缀 min 在线段树上二分的时候取就行。

code: /code/2022.4.21/P4364.cpp

[PKUWC2018]猎人杀

问题可以转化成向任何一个人开枪，如果这个人已经死了就再开一枪，直到打死人为止。

可以枚举钦定在 1 后死的人集合 S，那么答案就是 $\sum_S (-1)^{|S|} P(S)$。

其中 P(S) 是 S 集合内的人都在 1 后死的概率，也就等于 $\sum_{i=0}^{+\infty}(\frac{1-w_1-w_S}{w_{all}})^i\frac{w_1}{w_{all}}$，其中 $w_S$ 为 S 集合内 w 的和，$w_{all}$ 为所有 w 的和，用等比数列求和公式可以得到 $\frac{\frac{w_1}{w_all}}{\frac{w_1+w_S}{w_{all}}}=\frac{w_1}{w_1+w_S}$。

于是枚举 $w_s$ 发现 $f_i = \sum_S [w_S=i](-1)^S$ 的生成函数 $F(x)=\prod(1-x^{w_i})$，可以直接分治 NTT。

code: /code/2022.4.21/P5644.cpp